K近邻算法的Python实现

作为『十大机器学习算法』之一的K-近邻（K-Nearest Neighbors）算法是思想简单、易于理解的一种分类和回归算法。今天，我们来一起学习KNN算法的基本原理，并用Python实现该算法，最后，通过一个案例阐述其应用价值。

KNN算法的直观理解

（添加一个直观的图）

它基于这样的简单假设：彼此靠近的点更有可能属于同一个类别。用大俗话来说就是『臭味相投』,或者说『近朱者赤，近墨者黑』。

它并未试图建立一个显示的预测模型，而是直接通过预测点的临近训练集点来确定其所属类别。

K近邻算法的实现主要基于三大基本要素：

K的选择；
距离度量方法的确定；
分类决策规则。

下面，即围绕这三大基本要素,探究它的分类实现原理。

KNN算法的原理

算法步骤

K近邻算法的实施步骤如下：

根据给定的距离度量，在训练集 $T$ 中寻找出与 $x$ 最近邻的 $k$ 个点，涵盖这 $k$ 个点的 $x$ 的邻域记作 $N_k(x)$ ;
在 $N_k(x)$ 中根据分类决策规则决定样本的所属类别 $y$ :

$y = arg \ \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i = c_j), i = 1,2,\cdots,N;j = 1,2,\cdots,K.$

K的选择

K近邻算法对K的选择非常敏感。K值越小意味着模型复杂度越高，从而容易产生过拟合；K值越大则意味着整体的模型变得简单，学习的近似近似误差会增大。

在实际的应用中，一般采用一个比较小的K值。并采用交叉验证的方法，选取一个最优的K值。

距离度量

距离度量一般采用欧式距离。也可以根据需要采用 $L_p$ 距离或明氏距离。

分类决策规则

K近邻算法中的分类决策多采用多数表决的方法进行。它等价于寻求经验风险最小化。

但这个规则存在一个潜在的问题：有可能多个类别的投票数同为最高。这个时候，究竟应该判为哪一个类别？

可以通过以下几个途径解决该问题：

从投票数相同的最高类别中随机地选择一个；
通过距离来进一步给票数加权；
减少K的个数，直到找到一个唯一的最高票数标签。

KNN算法的优缺点

优点

精度高
对异常值不敏感
没有对数据的分布假设

缺点

计算复杂度高
在高维情况下，会遇到『维数诅咒』的问题

KNN算法的算法实现

import os 

os.chdir('D:\\my_python_workfile\\Project\\Writting')

os.getcwd()

'D:\\my_python_workfile\\Project\\Writting'

from __future__ import division
from collections import Counter
#from linear_algebra import distance
#from statistics import mean
import math, random
import matplotlib.pyplot as plt

# 定义投票函数
def raw_majority_vote(labels):
    votes = Counter(labels)
    winner,_ = votes.most_common(1)[0]
    return winner

以上的投票函数存在潜在的问题：有可能多个类别的投票数同为最高。

下面的函数则实现了解决方案中的第三种分类决策方法。

# 
def majority_vote(labels):
    """assumes that labels are ordered from nearest to farthest """
    vote_counts = Counter(labels)
    winner,winner_count = vote_counts.most_common(1)[0]
    num_winners = len([count 
                          for count in vote_counts.values()
                          if count == winner_count])
    if num_winners == 1:
        return winner
    else:
        return majority_vote(labels[:-1]) # try again wthout the farthest
    

# define distance function
import math

#### 减法定义
def vector_substract(v,w):
    """substracts coresponding elements"""
    return [v_i - w_i
                   for v_i,w_i in zip(v,w)]

def squared_distance(v,w):
    """"""
    return sum_of_squares(vector_substract(v,w))

def distance(v,w):
    return math.sqrt(squared_distance(v,w))

##########################################
# define sum_of_squares

### 向量的点乘
def dot(v,w):
    return sum(v_i * w_i 
                      for v_i,w_i in zip(v,w))


### 向量的平房和
def sum_of_squares(v):
    """v_1*v_1+v_2*v_2+...+v_n*v_n"""
    return dot(v,v)

# classifier
def knn_classify(k,labeled_points,new_point):
    """each labeled point should be a pair (point,label)"""
    
    # order the labeled points from nearest to farthest
    by_distance = sorted(labeled_points,
                        key = lambda (point,_):distance(point,new_point))
    
    # find the labels for the k cloest
    k_nearest_labels = [label for _,label in by_distance[:k]]
    
    # and let them vote
    return majority_vote(k_nearest_labels)

KNN算法的应用：案例分析

# 
cities = [(-86.75,33.5666666666667,'Python'),(-88.25,30.6833333333333,'Python'),(-112.016666666667,33.4333333333333,'Java'),
          (-110.933333333333,32.1166666666667,'Java'),(-92.2333333333333,34.7333333333333,'R'),(-121.95,37.7,'R'),
          (-118.15,33.8166666666667,'Python'), (-118.233333333333,34.05,'Java'),(-122.316666666667,37.8166666666667,'R'),
          (-117.6,34.05,'Python'),(-116.533333333333,33.8166666666667,'Python'),
          (-121.5,38.5166666666667,'R'),(-117.166666666667,32.7333333333333,'R'),(-122.383333333333,37.6166666666667,'R'),
          (-121.933333333333,37.3666666666667,'R'),(-122.016666666667,36.9833333333333,'Python'),
          (-104.716666666667,38.8166666666667,'Python'),(-104.866666666667,39.75,'Python'),(-72.65,41.7333333333333,'R'),
          (-75.6,39.6666666666667,'Python'),(-77.0333333333333,38.85,'Python'),(-80.2666666666667,25.8,'Java'),
          (-81.3833333333333,28.55,'Java'),(-82.5333333333333,27.9666666666667,'Java'),(-84.4333333333333,33.65,'Python'),
          (-116.216666666667,43.5666666666667,'Python'),(-87.75,41.7833333333333,'Java'),(-86.2833333333333,39.7333333333333,'Java'),
          (-93.65,41.5333333333333,'Java'),(-97.4166666666667,37.65,'Java'),(-85.7333333333333,38.1833333333333,'Python'),
          (-90.25,29.9833333333333,'Java'),(-70.3166666666667,43.65,'R'),(-76.6666666666667,39.1833333333333,'R'),
          (-71.0333333333333,42.3666666666667,'R'),(-72.5333333333333,42.2,'R'),(-83.0166666666667,42.4166666666667,'Python'),
          (-84.6,42.7833333333333,'Python'),(-93.2166666666667,44.8833333333333,'Python'),(-90.0833333333333,32.3166666666667,'Java'),
          (-94.5833333333333,39.1166666666667,'Java'),(-90.3833333333333,38.75,'Python'),(-108.533333333333,45.8,'Python'),
          (-115.166666666667,36.0833333333333,'Java'),(-71.4333333333333,42.9333333333333,'R'),(-74.1666666666667,40.7,'R'),
          (-106.616666666667,35.05,'Python'),(-78.7333333333333,42.9333333333333,'R'),(-73.9666666666667,40.7833333333333,'R'),
          (-80.9333333333333,35.2166666666667,'Python'),(-78.7833333333333,35.8666666666667,'Python'),(-100.75,46.7666666666667,'Java'),
          (-84.5166666666667,39.15,'Java'),(-81.85,41.4,'Java'),(-82.8833333333333,40,'Java'),(-97.6,35.4,'Python'),
          (-122.666666666667,45.5333333333333,'Python'),(-75.25,39.8833333333333,'Python'),(-80.2166666666667,40.5,'Python'),
          (-71.4333333333333,41.7333333333333,'R'),(-81.1166666666667,33.95,'R'),(-96.7333333333333,43.5666666666667,'Python'),
          (-90,35.05,'R'),(-86.6833333333333,36.1166666666667,'R'),(-97.7,30.3,'Python'),(-96.85,32.85,'Java'),
          (-98.4666666666667,29.5333333333333,'Java'),(-111.966666666667,40.7666666666667,'Python'),(-73.15,44.4666666666667,'R'),
          (-77.3333333333333,37.5,'Python'),(-122.3,47.5333333333333,'Python'),(-95.9,41.3,'Python'),(-95.35,29.9666666666667,'Java'),
          (-89.3333333333333,43.1333333333333,'R'),(-104.816666666667,41.15,'Java')]

cities = [([longitude,latitude],language) for longitude,latitude,language in cities]

# plot_state_borders

import re

segments = []
points = []

lat_long_regex = r"<point lat=\"(.*)\" lng=\"(.*)\""

with open("states.txt", "r") as f:
    lines = [line for line in f]

for line in lines:
    if line.startswith("</state>"):
        for p1, p2 in zip(points, points[1:]):
            segments.append((p1, p2))
        points = []
    s = re.search(lat_long_regex, line)
    if s:
        lat, lon = s.groups()
        points.append((float(lon), float(lat)))

def plot_state_borders(plt, color='0.8'):
    for (lon1, lat1), (lon2, lat2) in segments:
        plt.plot([lon1, lon2], [lat1, lat2], color=color)

# key is language, value is pair
plots = {"Java":([],[]),"Python":([],[]),"R":([],[])}

#mark and color
markers = {"Java":"o","Python":"s","R":"^"}
colors = {"Java":"r","Python":"b","R":"g"}

for (logitude,latitude),language in cities:
    plots[language][0].append(logitude)
    plots[language][1].append(latitude)
    
# create a scatter series for each language
for language,(x,y) in plots.iteritems():
    plt.scatter(x,y,color = colors[language],marker = markers[language],label = language,zorder = 10)
    
plot_state_borders(plt)

plt.legend(loc = 0)
plt.axis([-130,-60,20,55])

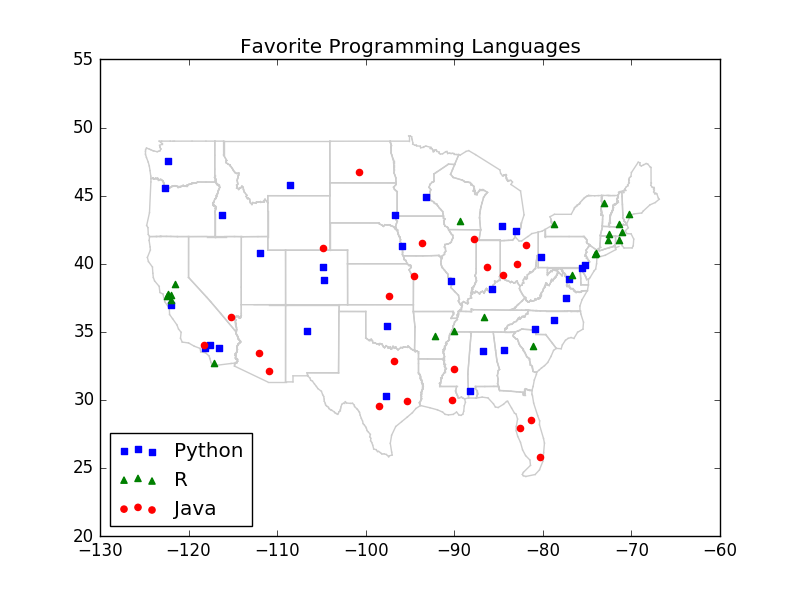
plt.title("Favorite Programming Languages")
plt.show()


    

# try several different values for k
for k in [1,3,5,7]:
    num_correct = 0
    
    for city in cities:
        location,actual_language = city
        other_cities = [other_city for other_city in cities if other_city != city]
        
        predicted_language = knn_classify(k,other_cities,location)
        
        if predicted_language == actual_language:
            num_correct += 1
            
    print k,"neighbor[s]:",num_correct,"correct out of ",len(cities)
        

neighbor[s]: 40 correct out of  75
neighbor[s]: 44 correct out of  75
neighbor[s]: 41 correct out of  75
neighbor[s]: 35 correct out of  75

参考文献

Grus J. Data Science from Scratch: First Principles with Python[M]. “ O’Reilly Media, Inc.”, 2015.